행렬
게임수학에서 행렬은 다방면으로 유용하게 사용되어 지고 있다.
기본적으로 벡터와 행렬을 같이 사용하는 경우가 많다.
예시로 캐릭터나 오브젝트이 좌표 자체는 위치벡터로 관리되어 지겠지만, 변화하는 과정 자체는 행렬로 연산되는것이다.

행렬의 연산
ㆍ행렬의 덧셈/뺄셈
크기와 모양이 같은 행렬은 원소 끼리 덧셈 및 뺄셈을 할수 있다.

ㆍ행렬의 곱
행렬의 곱은 크기와 모양이 다소 다른 행렬끼리도 계산이 가능하다.
이때의 조건은 앞에 곱하는 행렬의 행벡터와 뒤에 곱하는 행렬의 열벡터가 동일할때 행렬끼리의 곱을 할수 있다.
행렬 A가 m x n이고 행렬 B가 n x p이면 행렬곱인 AB가 가능하며 m x p의 행렬이 된다.

이 행렬의 곱은 교환법칙이 성립하지 않지만 교환법칙은 성립한다.

ㆍ대각행렬
행렬에서 행과 열이 일치하는 대각선에 위치하는 원소들을 대각요소라고 부른다.
행렬에서 이 대각요소에만 값이 주워지고 나머지 원소들의 값이 0일 경우 대각 행렬이라고 한다.

ㆍ단위행렬
위의 단위 행렬에서 대각요소들이 모두 1의값을 가지는 행렬을 단위 행렬이라고 한다.
이 단위행렬은 다른 크기가 맞는 행렬과 곱하면 곱한 자신이 값으로 나오게 된다.
또한 단위행렬은 교환법칙과 결합법칙이 성립된다.

ㆍ벡터와 행렬의 곱
위에서도 언급했듯 게임에서는 오브젝트이 위치는 위치벡터로 저장하고 이동 및 조정은 행렬과의 곱으로 수행된다.이때 뒤에 곱해지는 행렬은 MxM인 정사각형 행렬이 오게된다.예를 들자면 2차원공간의 좌표 v(x,y,1)은 1 x 3의 행렬이므로 행렬M(3x3)을 이용하여 계산이 되며,3차원 공간좌표 u(x,y,z,1)은 1 x 4의 행렬이므로 행렬 N(4x4)를 이용하여
ㆍ역행렬
역행렬은 임의의 행렬 A와 행렬 B를 곱한 값 AB가 단위행렬 I가 되었을때 A와 B는 서로 역행렬이다라고 할수있다.
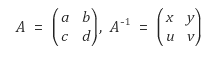

ㆍ전치행렬
전치행렬은 대각요소를 제외한 행과 열을 뒤바꾼 행렬이다.

위의 그림과 같이 M x N의 행렬은 N x M이 되며 대각요소를 제외한 모든 원소들을 뒤바꾼다.
또한 전치행렬을 2번 행할경우 자기자신이 나온다는 특징이 있다.
두행렬의 곱의 전치는 (MN)T=NTMT이다.
ㆍ직교행렬
직교행렬은 정방행렬A가 전치행렬인 AT와 역행렬인 A-1이 동일한 경우를 의미한다.
이러한 직교행렬은 역행렬을 구할때 많은 계산량이 요구되지만 전치행렬은 계산량이 적기 때문에 이를 이용한다.
게임에서는 x,y,z축이 서로 직교행렬이기에 계산량이 많은 역행렬 대신에 전치행렬을 이용하여 역행렬을 구하게 된다.
'게임수학 > 행렬' 카테고리의 다른 글
| 게임수학) Chapter6. World,View,Projection,Screen 행렬 (3) (0) | 2021.11.29 |
|---|---|
| 게임수학) Chapter6. World,View,Projection,Screen 행렬 (2) (0) | 2021.11.27 |
| 게임수학) Chapter6. World,View,Projection,Screen 행렬 (1) (0) | 2021.11.26 |
| 게임수학) Chapter5. 좌표계 변환행렬 (0) | 2021.11.17 |
| 게임수학) Chapter4. 변환행렬(SRT) (0) | 2021.11.17 |


댓글